simon77
Mitglied
- Beiträge
- 803
- Motorrad
- Brixton Cromwell 125
... ich überlege gerade, ob, warum und wie sich das Verdichtungsverhältnis auf die Leistung auswirkt.
Die zugeführte chemische Leistung (das zugeführte Benzin-Luftgemisch / Minute) ändert sich ja durch das Verdichtungsverhältnis überhaupt nicht.
In der Physik gibt es den Carnot-Prozess, der den "einfachsten" zyklischen Prozess einer Wärmekraftmaschine darstellt und den größten physikalisch möglichen Wirkungsgrad hat, der nur durch die Maximum- und Minimum-Temperatur in einem Zyklus gegeben ist.
Wärmekraftmaschine – Wikipedia
Eine höhere Verdichtung führt zu einer höheren Temperatur im Zylinder wodurch der Wirkungsgrad höher wird, und damit auch die Leistungsausbeute steigt.
Zitat aus obigem Wikipedia Link:
"Moderne" Motoren schaffen es schon dem Wirkungsgrad des Carnot-Prozesses recht nahe zu kommen, aber der Wirkungsgrad eines jeden Verbrennungsmotor ist durch den Carnot-Prozess beschränkt :
max Wirkungsgrad = 1 - (Temp-min / Temp-max)
Wie wirkt sich das Kompressionsverhältnis darauf aus?
... es wird verdammt kompliziert. Meine primitive und stark vereinfachte Herangehensweise wäre folgende:
In erster Näherung ist die Verdichtung eine Adiabatische Zustandsänderung (wie beim Carnot-Prozess) - bei reiner Luft würde das bedeuten:
T2 = T1 * (Kompressionverhältnis)^0,4
T2 ist die Temperatur direkt vor'm Zünden
T1 ist die Temperatur der Einlassluft
Alle Temperaturen in Kelvin ! (Kelvin = Grad Celsius + 273)
Und diese Temperaturen eingesetzt in den Wirkungsgrad des Carnot-Prozess (was ja laut Modell das einzige ist, was bei konstantem Hubraum zu einer Leistungssteigerung führt), ergeben folgendes:
Wirkungsgrad = 1 - Kompressionsverhältnis^(-0,4)
Jetzt hat's mich noch unter den Fingernägeln gejuckt, und ich habe diese Formel noch schnell geplottet:
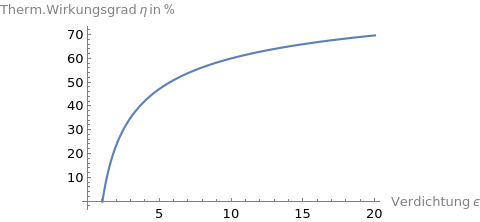
Man Vergleiche dies mit der Skizze aus der Fachliteratur von @Der Raucher
Die zugeführte chemische Leistung (das zugeführte Benzin-Luftgemisch / Minute) ändert sich ja durch das Verdichtungsverhältnis überhaupt nicht.
In der Physik gibt es den Carnot-Prozess, der den "einfachsten" zyklischen Prozess einer Wärmekraftmaschine darstellt und den größten physikalisch möglichen Wirkungsgrad hat, der nur durch die Maximum- und Minimum-Temperatur in einem Zyklus gegeben ist.
Wärmekraftmaschine – Wikipedia
Eine höhere Verdichtung führt zu einer höheren Temperatur im Zylinder wodurch der Wirkungsgrad höher wird, und damit auch die Leistungsausbeute steigt.
Zitat aus obigem Wikipedia Link:
"Moderne" Motoren schaffen es schon dem Wirkungsgrad des Carnot-Prozesses recht nahe zu kommen, aber der Wirkungsgrad eines jeden Verbrennungsmotor ist durch den Carnot-Prozess beschränkt :
max Wirkungsgrad = 1 - (Temp-min / Temp-max)
Wie wirkt sich das Kompressionsverhältnis darauf aus?
... es wird verdammt kompliziert. Meine primitive und stark vereinfachte Herangehensweise wäre folgende:
In erster Näherung ist die Verdichtung eine Adiabatische Zustandsänderung (wie beim Carnot-Prozess) - bei reiner Luft würde das bedeuten:
T2 = T1 * (Kompressionverhältnis)^0,4
T2 ist die Temperatur direkt vor'm Zünden
T1 ist die Temperatur der Einlassluft
Alle Temperaturen in Kelvin ! (Kelvin = Grad Celsius + 273)
Und diese Temperaturen eingesetzt in den Wirkungsgrad des Carnot-Prozess (was ja laut Modell das einzige ist, was bei konstantem Hubraum zu einer Leistungssteigerung führt), ergeben folgendes:
Wirkungsgrad = 1 - Kompressionsverhältnis^(-0,4)
Ergänzung ()
Jetzt hat's mich noch unter den Fingernägeln gejuckt, und ich habe diese Formel noch schnell geplottet:
Man Vergleiche dies mit der Skizze aus der Fachliteratur von @Der Raucher
Zuletzt bearbeitet:
)
)